Effective Proof-of-Stake
Harmony is one of the first production mainnets to feature a fully sharded PoS architecture. Across the 4 shards in Harmony mainnet, blocks are produced every 5 seconds and cross-shard transactions are finalized in 2 block times.
Harmony’s Effective Proof-of-Stake (EPoS) is the first staking mechanism in a sharded blockchain that achieves both security and decentralization. EPoS allows staking from hundreds of validators and the unique effective stake mechanism reduces the tendency of stake centralization. Meanwhile, stake delegation, reward compounding, double-sign slashing, and unavailability checking are also supported.
Our token economics model incentivizes early stakers with higher rewards to bootstrap the network successfully. For those validators or delegators who would like to join Harmony Open Staking, this guide will help you get started and learn about how everything works.
Effective stake is a new measure introduced in EPoS in order to prevent stake centralization and still provide capitalistic fairness. For exactly how it achieves that, here is the design rationale behind it.
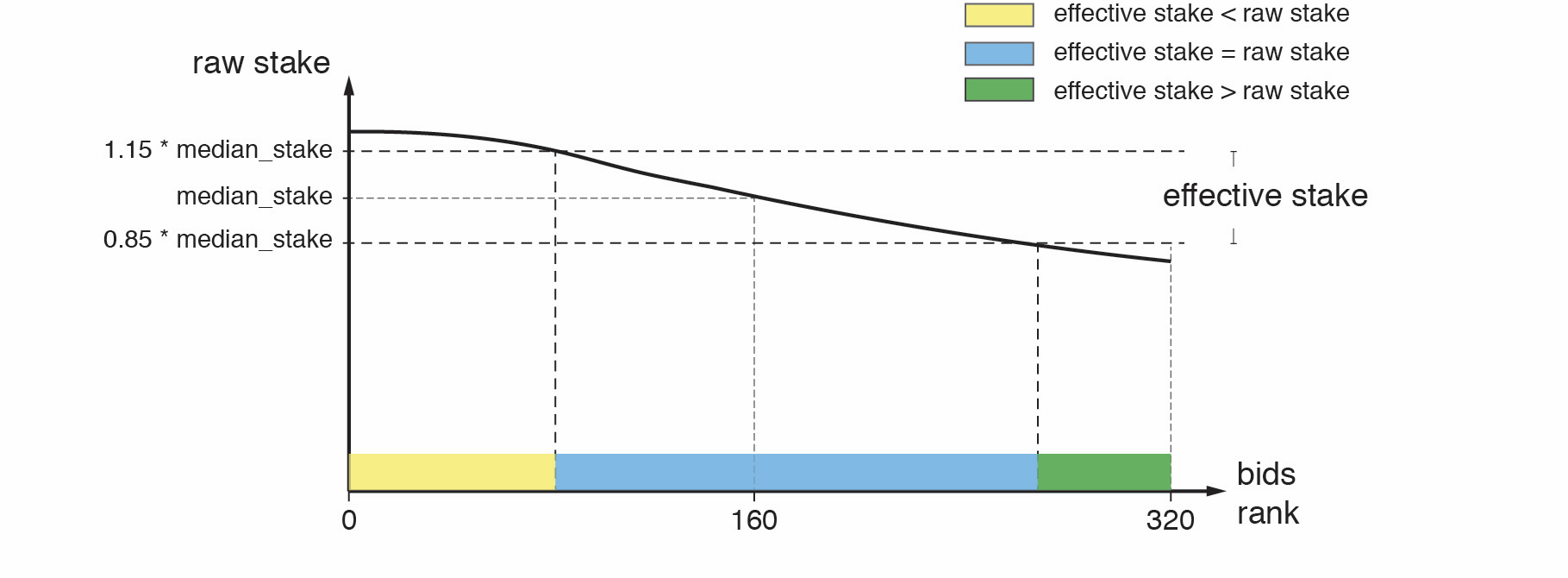
Let’s call the bid price of the elected BLS keys the raw stake. The effective stake of an elected BLS key is a bounded value on its raw stake with a threshold around the median bidder’s raw stake (denoted as median_stake in the picture below). The upper threshold is 115% of the median_stake and the lower threshold is 85% of the median_stake. For a key with raw stake that’s out of bound of the threshold, its effective stake will be bounded by the corresponding threshold, otherwise, the effective stake is the same as the raw stake.
The effective stake of each BLS key is determined at the last block of an epoch during the election process and will stay the same throughout the next epoch.
Effective Stake is Bounded around Median Stake
After the election and shard assignment, the BLS keys assigned in a shard become the committee of that shard. The voting power of an elected BLS key in a committee is the metrics used to measure the key’s weight in the consensus voting process. The total voting power of a shard committee is always 1.0 (or 100%). The consensus of a committee is only reached if more than 2/3 of the voting power is collected in the votes.
Each BLS key in the committee has a certain voting power proportional to the share of its effective stake among the whole committee. For example, if the sum of the effective stake of all the keys in the committee is 10k ONE, a BLS key with effective stake of 1000 ONE will have voting power 0.1 (or 10%).
For each of the blocks produced and confirmed within a shard, it should contain signatures from the keys with more than 2/3 of the total voting power of the shard committee. Each confirmed block will produce 7 ONE as block reward for the validators behind the committee. The 7 ONE is initially allocated to all the validators whose BLS key(s) signed on the block, proportionally to the voting power of the key(s) that signed.
The allocated block reward for a validator will be further distributed to delegators proportionally to their stake after the commission fee is charged. For example, a validator with a commission rate of 25% got allocated 4 ONE for a block it signed. The validator staked 1000 ONE itself and it has 2 delegations each with 1000 ONE. The block reward distribution for this validator works as follows:
- 1.The commission fee of 1 ONE (4 ONE * 25%) is cut from the original reward and credited to the validator.
- 2.The rest of the reward of 3 ONE is then distributed to all the stakers (including both the validator and its delegators) proportionally based on their stake. Since the stakers (the validator and the two delegators) each staked/delegated 1000 ONE, they each receive 1 ONE in the reward distribution.
If any BLS key(s) are detected signing conflicting blocks (i.e. blocks with the same height and view ID but with different block hashes), the validator will be slashed and forever banned from the network. When a validator is slashed, a certain percentage (i.e. slashing rate) of staked tokens from the validator and its delegators will be forfeited, of which half will be burnt and another half will be credited to the reporter of the double sign event.
The slashing rate is calculated by simply summing all the voting power of the double signing keys with a minimum of 2%. For example, if 3 BLS keys with voting power of 3%, 3% and 4% double signed at the same time, 10% of all staked tokens will be slashed on the validators who hold the 3 BLS keys.
The elected validators are obligated to validate blocks with their elected BLS keys. In every epoch, an elected validator should sign more than 2/3 of the signatures that its BLS keys are asked to sign.
The signing performance is represented by a percentage value called uptime. A validator’s uptime is the ratio of the number of signatures its elected BLS keys signed over the total number of signatures the keys should sign. For example, a validator has 2 elected BLS keys and each of the keys is presented 100 blocks to sign. In the final tally, the first key signed 70 blocks and the second key signed 80 blocks. Overall, the validator’s uptime is (70+80) / (100*2) = 75%.
At the end of each epoch, the validators with uptime of no more than 2/3 (66.66%) will have their status set to “Inactive” and be ruled out from the new election. For these inactive validators, they are required to manually set their status to “Active” by sending an EditValidator transaction in order to participate in future elections. We encourage validators to be proactive in maintaining a high uptime to ensure they remain elected and earn the most block reward possible.
Last modified 2yr ago